Specifications            Quick Tour            Tutorials            Reference            Forums

All basic operators (“+”, “-”, “*”, “/”, “±”, “√”, “^”, “x²”), and all functions from the Trigs, Logs, and Complex menus operate on complex numbers.

You can use complex numbers in RPL programs and expressions, either in literal form (i.e., as something like “(3,4)”) or in variables.

You can have expressions inside complex numbers, for their individual parts. Something like “(’7-4’, ‘a+5’)”. Such expressions must be evaluable and yield a Real Number by the time you apply an operator.

We will soon enable a third language in ND1, which will permit execution on the graphics processing unit (GPU) of compatible hardware (iPhone 3GS, iPod touch “3G”, iPad, for now) and permit the execution of millions of complex operations per second. You can view today what’s possible with this by looking at our Realtime Mandelbrot app, which utilizes this. (The two apps will soon be linked.)

Let’s try entering some complex numbers and doing operations on them.

Enter “(4, 7” (w/o quotes)

Enter “(8, 3” (w/o quotes)

Tap “*”.

This exercised complex multiplication.

Enter 5.

Go to the Trigs menu. Tap asin (ASIN).

As you see, some functions will return complex numbers in response to inputs that are out of the range of math with Real Numbers.

Enter -5. (Use the ± (CHS) key to enter the unary minus sign; before or after tapping five.)

Tap √x.

Did you know you can take the square root of a negative number? (They really ought to mention that in school...)

Enter ‘i’ (w/ quotes)

Tap the Eval key.

If you had entered ‘i’ w/o quotes, it would have evaled and enter as (0, 1) directly.

You can use complex numbers as points with rectangular (cartesian) or polar coordinates. Two complex numbers will add like ordinary points in 2-D, for example. (Just be mindful that multiplication is *not* scalar.)

Let’s do a real-world example (school book-style):

What distance is covered if you go 3 miles at an angle of 42°, followed by 5 miles at 70°, and what direction will you be headed?

Select the Mode menu via the ⌽ (MODE) key. (ND1: that’s over the ∿ key.)

Tap 360° (DEG) to switch to degree angle mode. (You may want to switch back to 2π (RAD), when you’re done with this tutorial. Results of the functions in Trigs (and some Logs), and functions that work with polar coordinates are depend on the current angle mode.)

Go to the Complex menu.

Enter 3

Enter 42

(3 miles, 42°; right now, we’re pretending these are polar coordinates (with length and angle parts))

Tap real→ (R→C).

(This is an alternative way to enter a complex number. We could have just entered it via (3, 42).)

Now let’s convert this into a rectangular (cartesian) point.

Tap polar→ (P→R) (Classic: Tap NEXT to display the next menu page.)

It is at this point, that we’re giving interpretation to (3, 42). Nothing was intrinsically “polar” about it before.

Now, for the second course segment:

Enter (5,70

Tap polar→ (P→R)

(this is the quick way to add polar coordinate pair)

Now add the two course segments as 2-D points:

Tap “+”

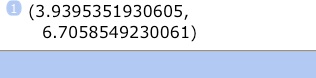
And change back to polar coordinates:

Tap →polar (R→P)

With that you converted back to polar representation and you’re done.

You covered 7.78 miles, and your heading is 59.57 degrees.